以遗传算法解最佳应援色排序问题

1.引言

现代应援界广泛采用电光棒进行应援。与传统化学棒相比，现代电光棒具有储存多种应援色、一键切换、发光时间长等优点。在 Live 中应援色变换用时问题是广大粉丝广泛关注的问题。不合理的应援色排序使应援色变换时按键次数增多，在较短时间内需要切换多种颜色时容易出错。因此对应援色排序进行优化，寻找一个最佳的排序是十分必要地。

遗传算法（Genetic Algorithm）为一种模拟自然界生物遗传与进化的自适应搜索算法，最早由密歇根大学的 Holland 教授于 1975 年提出。由于遗传算法具有容易实现、可并行处理、适应度函数适用范围广等优点，在系统设计、工业工程、神经网络等领域广泛使用。

本文提出一种考虑应援色变换次数的计算函数，应用遗传算法求解出最佳的应援色排序。

2.遗传算法

2.1 编码规则

2.1.1 互换编码

为方便计算机进行处理，需建立应援色与编码的映射关系。由于应援色多样且在一个序列中不重复，不能使用二进制编码。阅读文献^[1] 得知互换编码适用于旅行商问题、调度问题这种排序问题，因此选用互换编码。

以 Aqours 应援色为例，对色彩进行编码，如表1所示：

表1 应援色映射表

应援色	白	粉	黄	樱	柑	蓝	绿	红	紫
编码	0	1	2	3	4	5	6	7	8

2.1.2 所需换色表

一场 Live 期间各部分需切换应援色不同，需设计所需换色表。依每一部分所需切换应援色编排序列，如下所示：

5 3 4 5 -1 -1 -1 -1 -1
0 1 2 3 4 5 6 7 8
......

以一个节目为一列。假设最大换色次数为9，对于不足位用 -1 来填充数组中空位，统计次数函数遇 -1 完成一次计算。由于本问题为排序问题，因此采用互换编码。针对互换编码选用单交叉点法交叉、逆转变异算子变异。

2.2 计算策略

2.2.1 数据结构

以广泛使用的 King Blade 系列电光棒进行分析，观察 King Blade X10 III（以下简称KBX3）电光棒应援色变换过程，其具有正向、反向变换按钮，可以在设定数量应援色序列中循环变换。因此采用双向循环链表数据结构。构造链表如图1所示：

图1 链表示意图

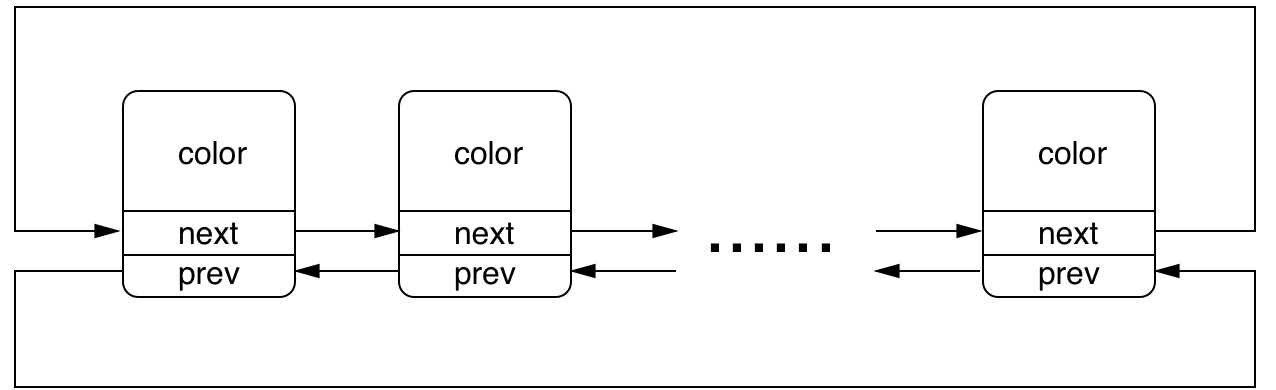
2.2.2 统计函数

KBX3 变换颜色时每按动一次按钮，变换一次颜色，因此设计统计函数统计按键次数，以按键次数少的为优。

统计函数：以最终停留应援色位为起始点，分别顺时针、逆时针检索需变换的下一应援色。比较两向所用变换次数，选择所用次数较少方向，累加其次数。循环直到统计完全部所需颜色。

2.3 算法描述

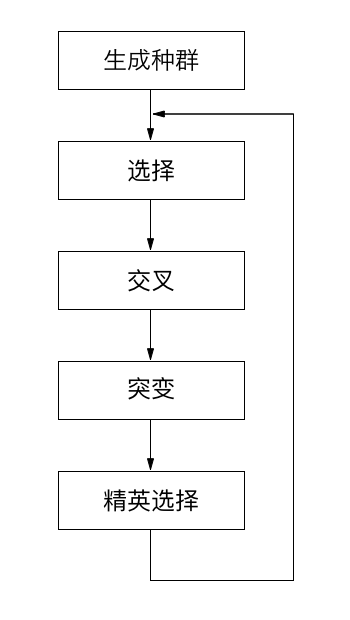
图2 算法示意图

3.数值模拟

以 Aqours 1st Live 所需变换颜色与个人偏好设定所需应援色表。如下所示：

0,-1,-1,-1,-1,-1,-1,-1,-1
5,3,4,5,-1,-1,-1,-1,-1
0,1,2,3,4,5,6,7,8
0,-1,-1,-1,-1,-1,-1,-1,-1
0,4,-1,-1,-1,-1,-1,-1,-1
4,2,0,-1,-1,-1,-1,-1,-1
0,-1,-1,-1,-1,-1,-1,-1,-1
3,-1,-1,-1,-1,-1,-1,-1,-1
0,-1,-1,-1,-1,-1,-1,-1,-1
0,5,-1,-1,-1,-1,-1,-1,-1
0,-1,-1,-1,-1,-1,-1,-1,-1

设定交叉率0.9，突变率0.05。种群大小800，迭代次数500，进行测试。

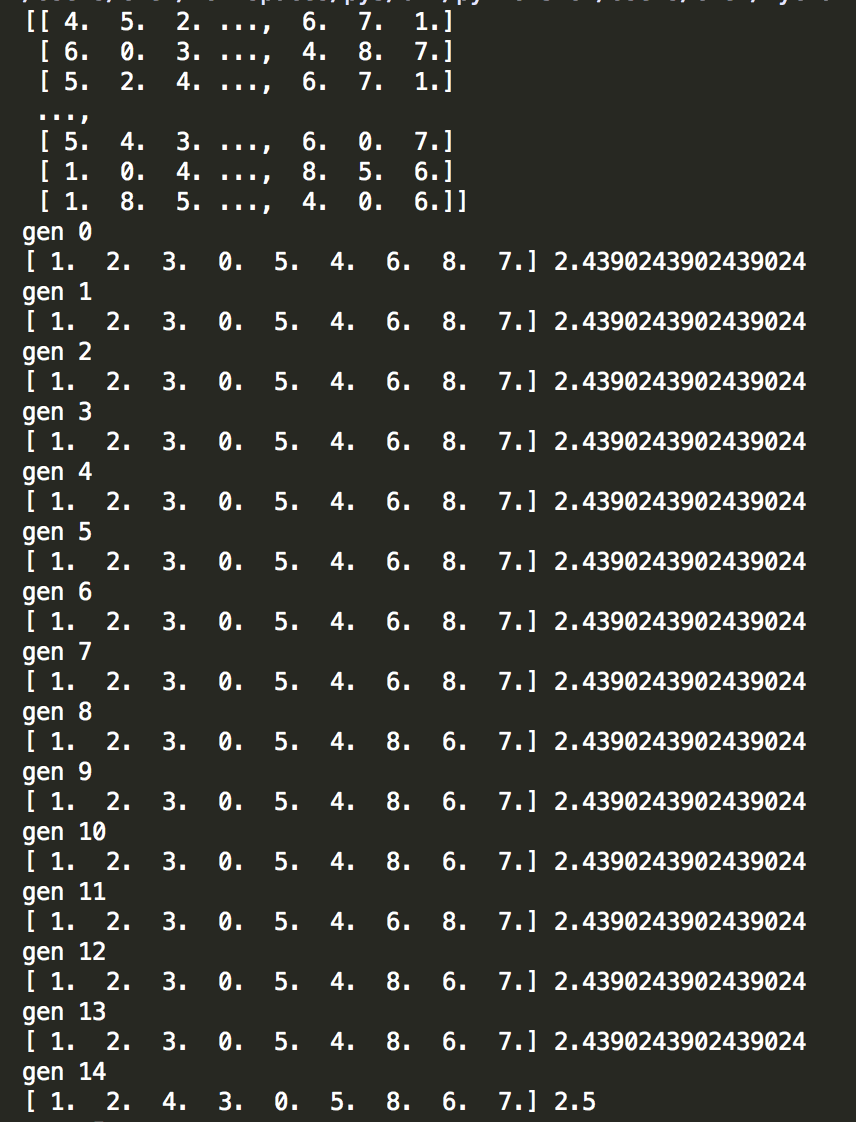
图2 测试起始图（依次为种群染色体序列，每一代最优个体序列、适应度）

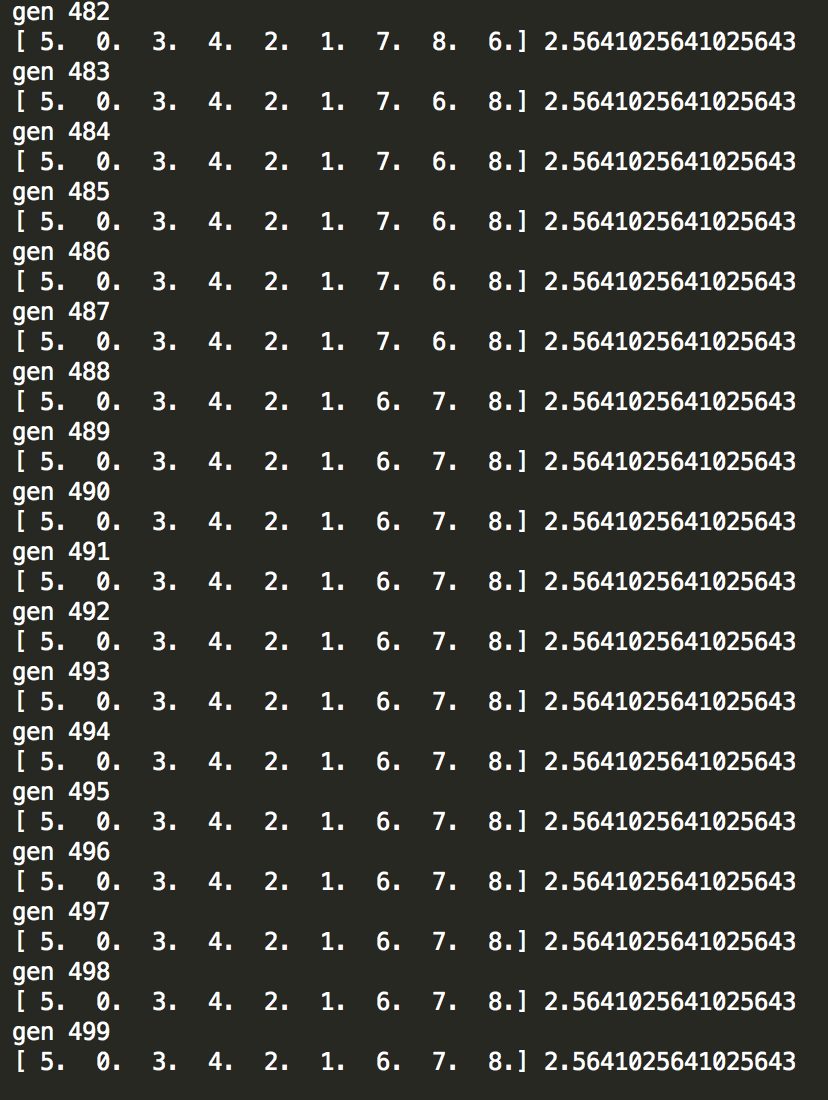
图3 测试迭代完成图

由图 2 可见起始时最优适应度为 2.439，在第 15 代适应度增为 2.5。由图3可见最终获得最优适应度 2.564。观察整个过程，2.439 的为第1～14代，2.5 的为第 15～230 代，2.564 的为 231～500 代。可见在最初时适应度增加迅速，后期较早收敛，第232代后不再变化。推测种群较大可较早获得最佳个体，可按种群规模适当减少迭代次数。

将遗传算法取得最优个体序列（5，0，3，4，2，1，6，7，8）与MC顺序序列（0，1，2，3，4，5，6，7，8）进行比较，遗传算法序列切换 39 次，MC序列切换 48 次，可见遗传算法获得显著减少切换次数的排序。

5.结论

通过测试得出如下结论：

• 1. 使用遗传算法获得最佳排序，优于普通排序。可以有效地解决最佳应援色排序问题。
• 2. 遗传算法虽然获得最佳排序，但有时较早收敛，有无效迭代。

参考文献

1. Murata T, Ishibuchi H, Tanaka H. Genetic algorithms for flowshop scheduling problems[J]. Computers & Industrial Engineering, 1996, 30(4): 1061-1071. ↩